1. 이차방정식과 근의 공식
이차방정식이란 최고 차항의 차수가 2인 방정식, 그러니까 지수가 가장 큰 항의 지수가 2인 방정식으로, 중학교 3학년 1학기 과정에 등장하는 내용이며, 일반적으로 ax²+bx+c=0이라는 형태로 나타낸다.
일차방정식의 경우, 그 형태가 비교적 단순하여, 어렵지 않게 한 개의 해를 구할 수 있다.
하지만 이차방정식이나 그 이상의 고차방정식의 경우, "인수분해", 혹은 "근의 공식"이라는 방법 중 하나를 이용해 근을 구해야 한다.
여기서 주의해야 할 점은, n차 방정식의 경우 그 근의 개수가 n개까지 존재할 수 있다는 점인데,
이차방정식은 근의 개수가 0개(허근), 1개(중근), 2개(서로 다른 실근) 일 수 있다. 풀이 방법 중 하나인 인수분해는 이차식을 두 개의 일차식의 곱의 꼴로 바꿔 각각의 일차방정식을 풀어주는 방법이며, 근의 공식이란 인수분해가 불가능할 경우 어떤 공식에 각 항의 계수를 대입하여 근을 직접적으로 구하는 방법이다.
그리고 오늘 알아볼 것은 근의 공식 유도이다.
이전 게시글인 피타고라스에서는 증명보다 서론이 길었는데, 그래서 이번 게시글에서는 증명과 활용을 위주로 작성하도록 하겠다.
2. 근의 공식의 증명과 활용
일단 ax²+bx+c=0 이라는 이차방정식의 근은
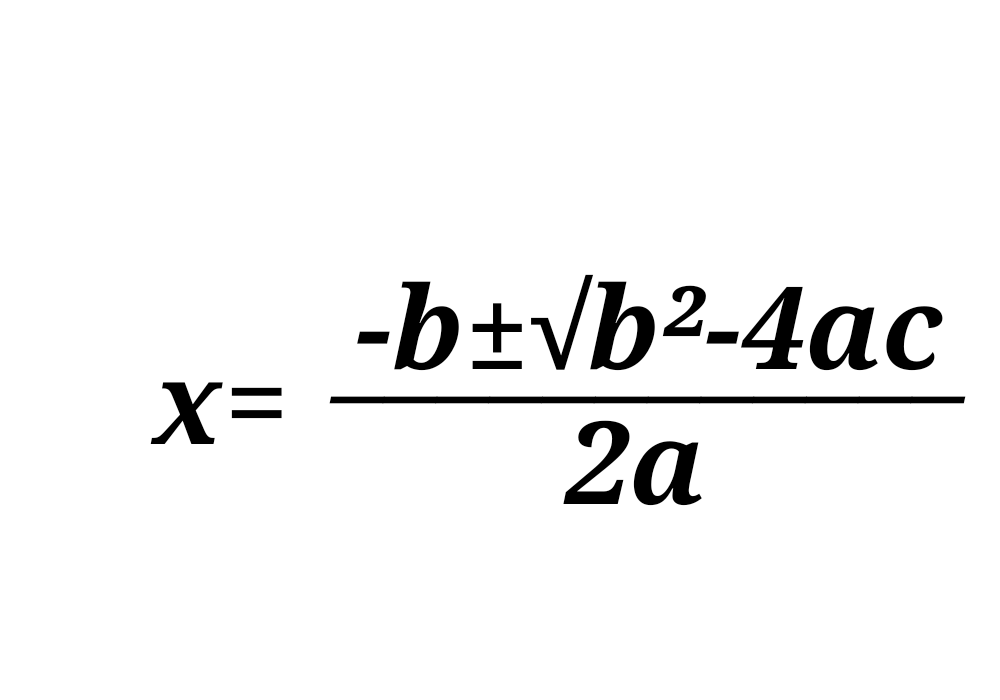
이러한 형태로 나타낼 수 있고, 이것이 근의 공식이다. 수학을 좀 해보신 독자분들이라면 아마 꽤나 익숙할 것이다. 복잡해 보일 수 있지만, 이걸 유도하는 방법은 의외로 간단하다.
pf.
우선 ax²+bx+c=0을 변형해보겠다.
우선 x²항과 x항을 a로 묶어주면,
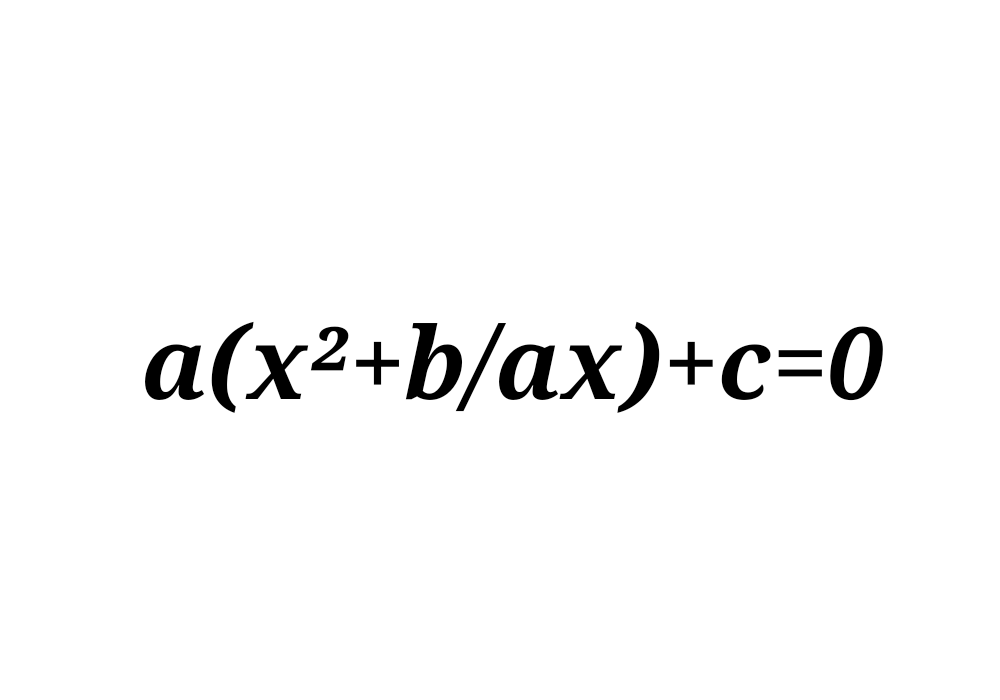
괄호 안의 식을 "완전제곱식"으로 변형해줄 것이다.
완전제곱식이란, 인수 분해했을 때 어떤 일차식의 제곱 꼴로 나타내어지는 식을 일컫는 말이다.
예컨대, (a+b)²=a²+2ab+b² 같은 식을 완전제곱식이라고 하는 것이다.
x²+b/ax를 완전 제곱식으로 만들려면, x항의 계수를 2로 나누고, 그 값을 제곱한 값을 더해줬다가 빼주면 된다.
따라서

이 식을 그대로 대입해주자.
a(x+b/2a)²-(b²/4a²)a+c=0
완전제곱식을 제외한 항을 이항해주고,
a(x+b/2a)²=b²/4a -c
양변을 a로 나눠준다.
(x+b/2a)²=(b²-4ac)/4a²
여기에 제곱근을 씌워주면,
x+b/2a=±√(b²-4ac)/2a
여기서 플러스 마이너스는 뒤의 값에 양의 부호가 붙은 값과 음의 부호가 붙은 값을 한 번에 나타낸 기호이며, 이게 붙는 이유는 b²-4ac의 제곱근은 +√b²-4ac와 -√b²-4ac로 두 가지가 있기 때문이다.
그럼 이제 마지막으로 b/2a를 이항하자.
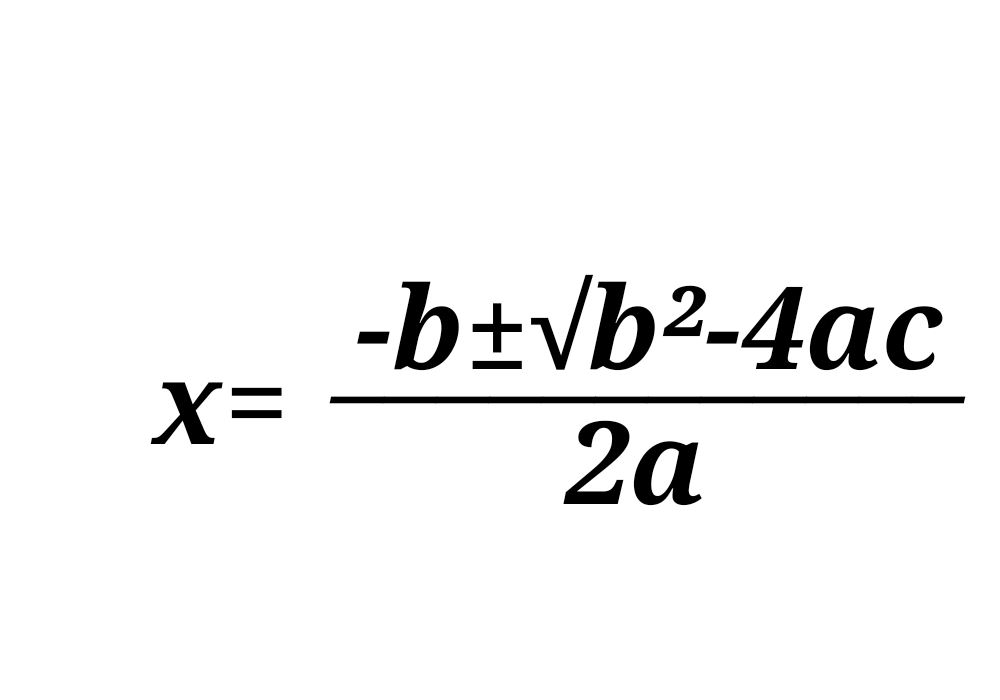
근의 공식은 이렇게 전개된다.
Q.E.D
이렇게 전개된 근의 공식이 근을 알맞게 구할 수 있는지 확인해보도록 하자.
x²+5x+6=0을 예로 들어보겠다.
이러한 형태의 이차방정식의 경우 정수의 인수분해만으로도 손쉽게 근을 구할 수 있다.
하지만 필자는 방금 구한 근의 공식을 이용해 이차방정식을 풀어보겠다.
x=(-5±√(5²-4•1•6))/2•1=(-5±√1)/2=(-5±1)/2=-3 or -2
근의 공식에 의하면 이 방정식의 근은 x=-2 또는 x=-3이다.
그럼 검산을 위해 x=-2와 x=-3을 아까의 이차방정식에 대입해보자.
(-2)²+5•(-2)+6=4-10+6=0
(-3)²+5•(-3)+6=9-15+6=0
등식이 성립하는 것을 알 수 있다.
이러한 근의 공식은 어떤 이차방정식에 대해서도 성립하는 공식인데,
b가 짝수일 경우에는 b=2b'로 두어 다음과 같이 더 간단하게 변형시킬 수도 있다.

이렇게 구한 근의 공식은 고등학교 수학(상) 과정에서 근과 계수의 관계, 판별식 등에 사용되기도 한다.
예를 들어 근과 계수의 관계는, ax²+bx+c=0에서의 두 근의 합과 곱을 계수에 관한 식으로 다음과 같이 나타내어 주는 것이고,
이차방정식 ax²+bx+c=0의 근이 α, β일 때,
αβ=-b/a
α+β=c/a
(근의 공식에서 구한 근을 각각 곱해주고 더해주면 쉽게 증명 가능하다.)
판별식이란 앞서 구한 근의 공식에서 b²-4ac가 양수냐, 0이냐, 음수냐에 따라서 근의 개수를 알 수 있게 해주는 식이다.
판별식은 D=b²-4ac로 나타내는데,
예를 들어 D>0일 경우에는 제곱근의 값이 두 가지 존재하기 때문에 두 개의 실수 근, 그러니까 실근을 가지게 되고, D=0일 경우에는 루트 안에 0이 들어가기 때문에, 두 근이 아닌 한 개의 실근, 그러니까 중근을 가지게 되며, D<0일 경우에는 제곱근 안에 음수가 들어가게 되는데, 실수 범위에서는 제곱하여 음수가 되는 수가 존재하지 않기 때문에, 중등과정에서는 b²-4ac가 음수일 때 근이 존재하지 않는다고 배운다. 고등학교 수학에서는, 유리수와 무리수를 통틀어 일컫는 실수 범위에 허수라는 제곱하여 음수가 되는 가상의 숫자를 추가하여 복소수 범위까지 수체계를 확장하게 되지만
그냥 b²-4ac의 값이 음수일 경우에는 실수 범위에서 해를 구할 수 없다고 생각하면 된다.
이전에 피타고라스에서도 언급했듯이, 필자는 이 게시글에서의 수학적 오류나 알맞지 않은 표현들을 지적하는 여러분들을 말리지 않을 것이다. 오늘은 이차방정식의 근의 공식을 유도하는 방법을 작성해 보았다. 근의 공식도 피타고라스와 같이 어떠한 이차방정식에 대해서도 성립하는 절대적인 공식이다. 근의 공식은 우리가 수학적인 증명을 하거나 문제를 풀 때 수식을 매우 간단하게 만들어주기도 한다. 이차방정식의 근의 공식 말고도 삼차방정식, 사차방정식의 근의 공식까지는 존재하지만, 그것들은 이차방정식의 근의 공식에 반해 그 형태가 매우 매우 복잡하여, 웬만한 이과생들도 잘 외우지 않고, 고등학교 과정에서도 배우지 않는다. 삼차방정식의 근의 공식은 추후에 업로드해볼 것이며, 게시글을 읽어주신 여러분들께 감사의 말씀을 드린다.
'수학' 카테고리의 다른 글
| "진짜" 확률 계산하는 방법 (0) | 2024.04.02 |
|---|---|
| [ANDRY](짧은 글)y=x^a꼴의 다차함수에서 x가 자연수일때 함숫값의 증가량의 변화 (0) | 2022.08.13 |
| [ANDRY]자연상수 e의 계산 (0) | 2022.06.03 |
| [ANDRY]피타고라스 정리 (0) | 2022.05.26 |
